XGSLab

Modules

XGSLab includes the modules:

• GSA (GROUNDING SYSTEM ANALYSIS) for basic application with underground systems
• GSA_FD (GROUNDING SYSTEM ANALYSIS in the FREQUENCY DOMAIN) for general applications with underground systems
• XGSA_FD (OVER AND UNDERGROUND SYSTEM ANALYSIS in the FREQUENCY DOMAIN) for general applications with overhead and underground systems
• XGSA_TD (OVER AND UNDERGROUND SYSTEM ANALYSIS in the TIME DOMAIN) for general applications with overhead and underground systems
• NETS (NETWORK SOLVER) to solve full meshed multiconductors networks
• SHIELD (Lightning Shielding) graphical application for the evaluation of the protection of structures from direct lightning strokes

 

The modules GSA, GSA_FD, XGSA_FD and XGSA_TD integrate the module SRA (Soil Resistivity Analysis) and XGSA_TD integrates also the module FA (direct / inverse Fourier Analysis).

The application field of these four modules is wide because they are based on the PEEC (Partial Element Equivalent Circuit) method, a numerical method for general applications powerful and flexible and perfectly suitable for engineering purposes.

This method allows the analysis of complex scenarios including external parameters such as voltages, currents and impedances.

The implemented PEEC method solves the Maxwell equations in full wave conditions taking into account the Green functions for propagation, the Sommerfeld integrals for the earth reaction, the Jefimenko equations for electric and magnetic fields and moving from the frequency to the time domain by means the Fourier transforms.

These four modules can import data from “dxf” files, and also export data and results in “dxf” files with a full interactivity with CAD tools.

The module NETS is based on the phase components method and integrates specific routines for the calculation of the parameters of lines, cables and transformers.

The module SHIELD is based on a 3D graphical application and consider the most diffused algorithm for the evaluation of the protected volume from lightning strokes.

All modules are integrated in an “all in one” package and provide professional numerical and graphical output useful to investigate any electromagnetic greatness.

All algorithms implemented in XGS are highly efficient in terms of computation speed and have been validated and tested by many Customers in the world.

XGS is easy to use by engineers who need not to be necessarily experts in the specific field, and moreover accurate, stable and fast.

Everything possible has been done to enhance user friendliness and increase productivity to this powerful tool.

 

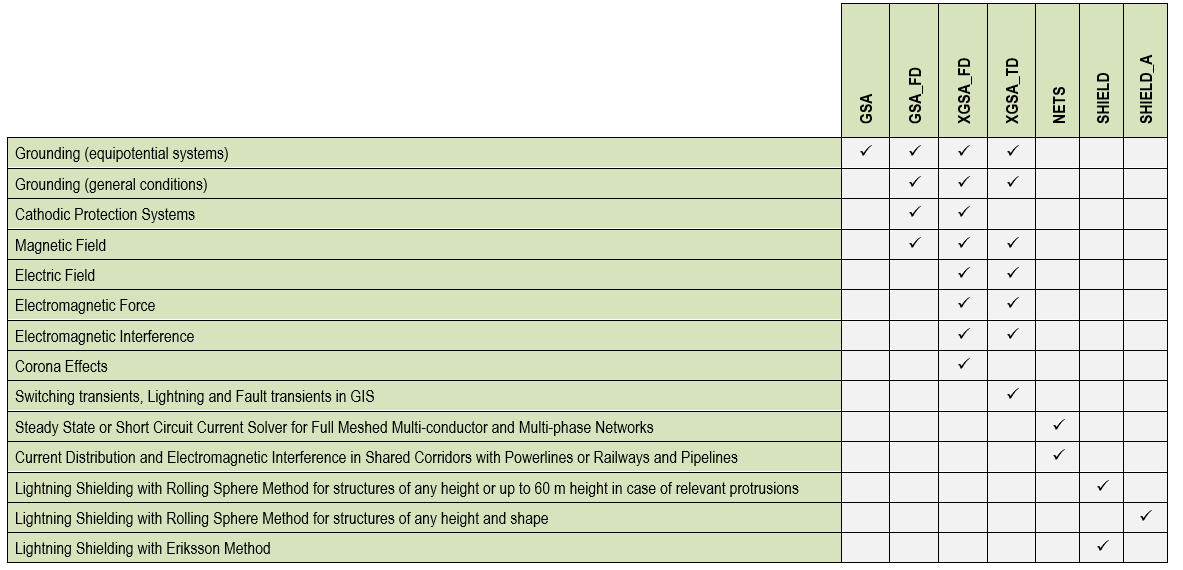
Applications of the different modules

The following table summarizes the main applications of GSA, GSA_FD and XGSA_FD.

 

 

XGSA_TD can be applied in order to analyse current and potential distribution in the time domain on underground and/or overhead conductors energized by means of current or voltage transient. Moreover, XGSA_TD can calculate the distributions of earth potentials and electric and magnetic fields in the time domain.

NETS is a tool based on circuit theory and then it is completely different form the other modules XGSLab modules based on the electromagnetic fields theory.
NETS can solve full meshed multi-conductor and multi-phase networks composed of multi-port cells connected by means of multi-port buses.
NETS can calculate potentials and currents in all ports in steady state or fault conditions and in particular can be used for the calculation of the fault current distribution in power networks.

GSA_FD

GSA_FD is a module for earth grid calculation and design in the frequency domain, including soil resistivity analysis and represents the state of the art of grounding software.
GSA_FD is based on a PEEC full wave numerical model and can be applied in general conditions with systems composed by many distinct electrodes of any shape, size and kind of conductor (solid, hollow or stranded and coated or bare) into a uniform, multilayer or multizone soil model in a large frequency range from DC to about 100 MHz. It is moreover important to consider that GSA_FD is able to takes into account the frequency dependence of soil parameters according to many models models and in particular in the model with a general consensus indicates in the CIGRE TB 781 2019.
GSA_FD allows the analysis of large electrodes whose size is greater than the wavelength of the electromagnetic field as better specified in the following. GSA_FD then overcomes all limits related to the equipotential condition of the electrodes on which GSA is based. With the equipotential condition hypothesis, the maximum touch voltage is widely underestimated and this may result in grounding system oversizing with additional cost sink even 50%.
The implemented model considers both self and mutual impedances. Experience shows that often, mutual impedances cannot be neglected not even at power frequency. A few competitors take into account self impedance and a very few competitors consider the mutual impedance effects and this can lead to significant errors in calculations. Neglecting self impedance effects is often unacceptable, but neglecting mutual impedances can lead to errors over the 20% in calculations also at power frequency. It is important to consider that calculation accuracy often means saving money and indeed, so GSA_FD can allow a significant cost saving in grounding system construction and materials.
GSA_FD can also calculates magnetic fields due to grounding systems or cable, and electromagnetic interferences (induced current and potential due to resistive, capacitive and inductive coupling) between grounding systems or cable and pipeline or buried electrodes in general.
In DC conditions, GSA_FD is a good tool for cathodic protection and anode bed analysis with impressed current systems.

Read more ...

XGSA_FD

XGSA_FD extends the GSA_FD application field to the overhead systems.
Also XGSA_FD is based on a PEEC full wave numerical model and can be applied in general conditions in the same frequency range of GSA_FD.
XGSA_FD can also manage catenary conductors and bundle conductors too and can take into account sources where potential or leakage current and longitudinal current are forced and independent by other conditions. For these reasons XGSA_FD is probably one of the most powerful and multipurpose tool on the market for these kind of calculations.
In addition to GSA_FD, XGSA_FD can calculate electromagnetic fields and interferences between over and under ground systems (for instance between overhead or underground power lines and installation as pipelines, railways or communications lines).
XGSA_FD integrates a powerful tool for the evaluation of the corona effects (power losses and radiofrequency interferences).

Read more ...

XGSA_TD

XGSA_TD is a powerful module which extends the XGSA_FD application field to the time domain.
In this regard, XGSA_FD uses the so called “frequency domain approach”. This approach is rigorous and allows considering the frequency dependence of soil parameters.
As known, a transient can be considered as the superposition of many single frequency waveform calculated with the forward Fast Fourier Transforms (FFT).
Using the frequency domain PEEC model implemented in XGSA_FD it is then possible calculate a response for each of these single frequency waveform.
The resulting time domain response can be obtained by applying the Inverse Fast Fourier Transform to all these responses calculated in the frequency domain.
The calculation sequence implemented in XGSA_TD is also called FFT – PEEC – IFFT.
XGSA_TD has been tested for the simulation of transients with a maximum frequency spectrum up to 100 MHz and then can be used for switching transients, lightning and also in fault transients in GIS.
XGSA_TD includes an option to export frequency dependent self and mutual impedances to EMTP® or ATP® in order to simulate with a rigorous model the dynamic behaviour of large grounding systems during electromagnetic transients.

Read more ...

NETS

NETS is a very flexible tool able to solve full meshed multi-conductor and multi-phase networks taking into account all the neutral conductors paths as well as the earth path.
NETS is based on the phase components method (and then on Kirchhoff laws) and graphs theory for multi-conductor and multi-phase systems.
The phase components method is general and overcomes the limits of the classic sequence components method.
The sequence component method is well established since 1918, but it can be used only with symmetrical systems or for systems quasi-symmetrical like the common transmission power lines (overhead lines and cables) or transformers. Non-symmetrical conditions could happen, for instance in case of power lines when the phase geometry is not equilateral and transposition is not used.
Moreover, the sequence component method cannot be used in case of multiple grounded systems or in case of problems that involve currents to earth.
The phase components method can be used to represent power systems as multi-conductor networks enabling the consideration of non-symmetrical systems also in presence of multiple grounding circuits.
The network components (generators, lines, cables, transformers, loads, switches, faults …) are represented using multi-port cells and the connection between cells is obtained by means of multi-port buses.
NETS considers also a special hybrid cell where cables, lines and conductors (pipes, rails, couterpoises …) can be combined in a single multi-port cell. This special cell can be useful for the evaluation of electromagnetic interferences in case of powerline or railways corridors and the calculation of current distribution in railways.
The grounding systems (substation grids, tower footings …) can be specified in an arbitrary way.
NETS calculates lines, cables and transformers parameters starting on data usually available in commercial data sheet.
NETS includes a converter from the sequence domain to the phase domain. This tool can converts sequence impedances matrix to phase impedance matrix.
Like the other XGS modules, also NETS has been thought for a use as general as possible.
NETS can be used to solve transmission and distribution networks in steady state or fault conditions and to calculate potentials and currents or any kind of short circuit currents with or without fault impedances.
In particular, NETS can be used for the calculation of the fault current distribution in power networks and between power circuits and earth. An accurate knowledge of the fault current distribution is crucial in grounding, mitigation to reduce interference on communication circuits and pipelines, power systems protections calibration and coordination, neutral grounding resistor sizing and many other applications.
NETS is also useful to calculate data input for other XGS modules (for instance the split factor and the current to earth) without unrealistic assumptions as for instance, magnitude of fault current known and unaffected by grounding impedances, impedances of overhead earth wires or tower footing resistances uniform along the line, or again, infinite length of lines …
Moreover, NETS represents the link between XGS and the most diffused commercial software for power systems analysis.

Read more ...

 

SHIELD

SHIELD is a powerful full 3D graphical application for the evaluation of the protection of structures from direct lightning strokes using the Rolling Sphere and the Eriksson methods.

SHIELD takes into account International (IEC 62305-3:2012), European (EN 62305-3:2012) and American (IEEE Std 998-2012) Standards but as known, the Rolling Sphere Method is considered by many other standards (NFPA, AS …).

When the Rolling Sphere Method is set, SHIELD first generates a 3D surface corresponding to all possible points that can be touched by the surface of the sphere with a specific radius as it rolls over the air termination system.

The air termination system can be composed of any combination of masts and wires (catenary wires included). This surface defines the protected volume.

The protected volume is then superposed to the structure to be protected. The parts of the structure to be protected that protrudes over this surface are not protected.

If the method is applied to the structure to be protected, it can identify the possible lightning strokes impact points and gives indications for the air termination positioning.

When the Eriksson Method is set, SHIELD generates the collection area of air termination system and structure to be protected.

The lightning protection system is effective when collection area of air termination system includes collection area of structure to be protected.

The User can modify the lightning protection system and generate again the protected volume or collection areas.

Read more ...

Applications

 

APPLICATIONS

Product Comparison Chart

 

PRODUCT COMPARISON CHART 

 

Comparing GSA to GSA_FD

The following table summarizes the main assumptions on which GSA and GSA_FD module are based.

 

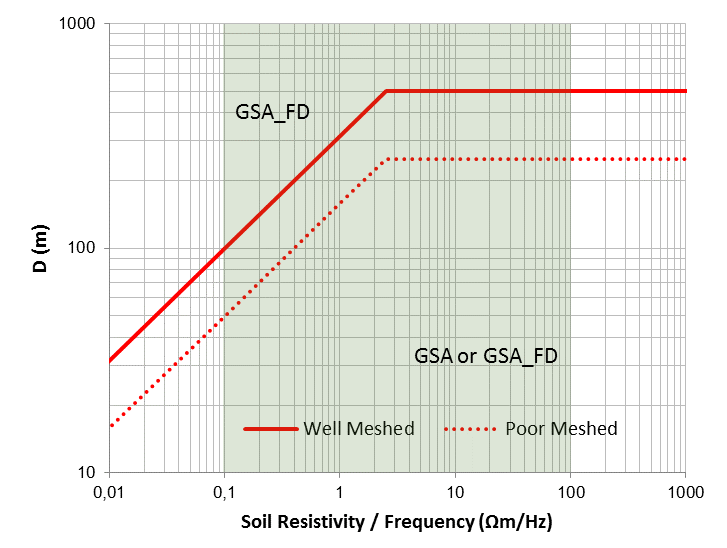
The following diagram represents the application domain of the two modules. The highlighted central area indicates the usual condition at power frequency.

The diagram has been obtained from a parametric analysis using square well-meshed copper grids energized with a current injected in a corner. The analysed parameters were the grid diagonal “D”, the soil resistivity and the frequency.

In its application dominion as defined by the red solid line, the error made by GSA in the GPR and touch voltages calculation is lower than about 10%.

Application domain of GSA and GSA_FD

In practice, in case of well-meshed grids, application limits of GSA can be defined as a function of the wavelength of the electromagnetic field in the earth as follows:

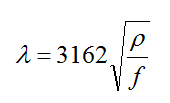
where λ (m) = wavelength, ρ (Ωm) = soil resistivity and f (Hz) = frequency.

The previous diagram indicates that GSA can be used if “D < λ/10”.

GSA also requires “D < 500 m” as reasonable limit.

The application limits will be lower if the grid shape is not regular, if the meshes are sparse and if the grid is made of steel or other high resistivity metal. In all these cases, the limit related to poor-meshed grids as defined by the red dashed line should be considered.

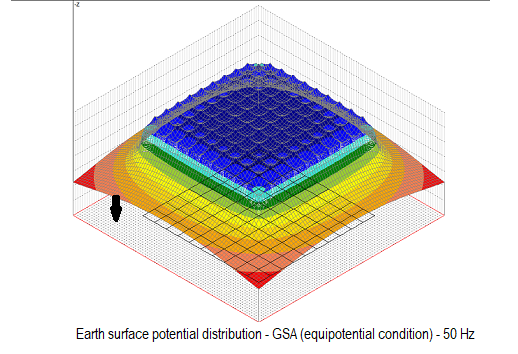
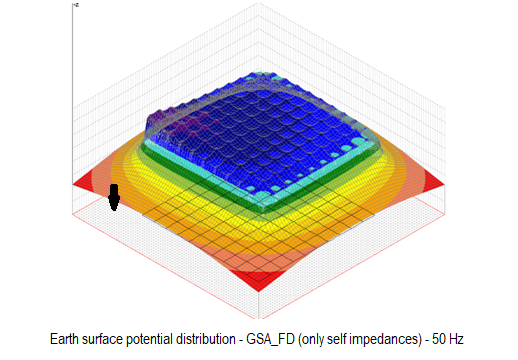
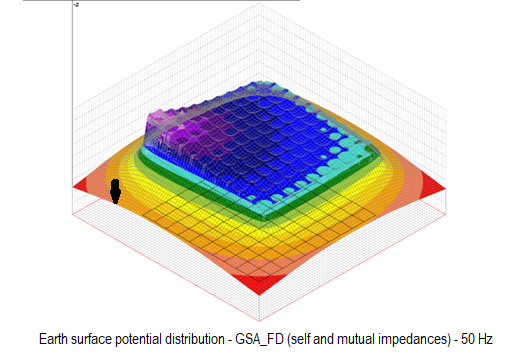
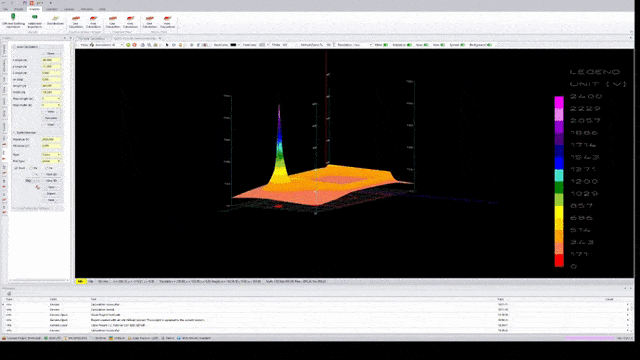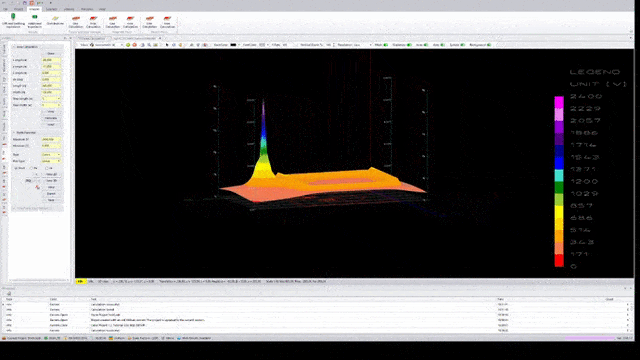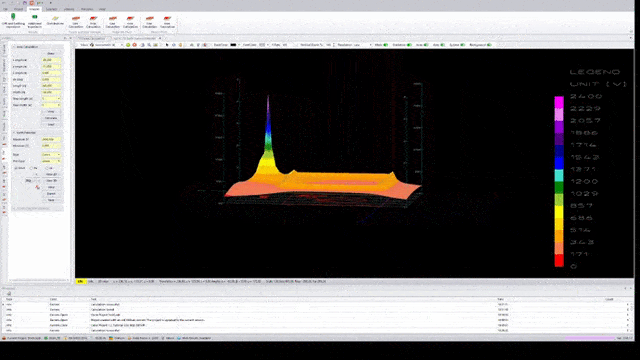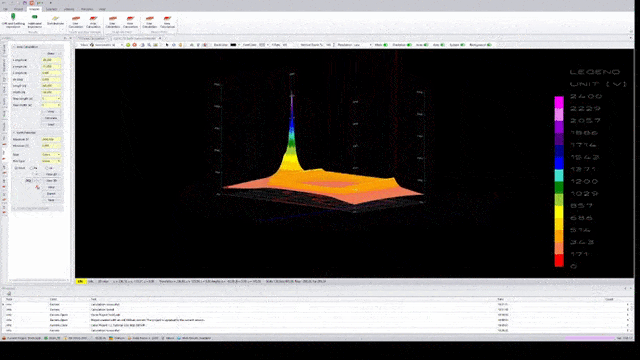
The following three figures show the earth surface potential distribution calculated by applying GSA and GSA_FD to a 100 m x 100 m grid with the same injected current, the same frequency (50 Hz), the same injection point (marked with arrow) and the same soil model.

The qualitative difference between results is evident. GPR and impedance to earth tend to grow whether self impedance and mutual impedance are taken into account. High frequency or low soil resistivity can make this difference even more evident.

Of course, a difference in the earth surface potential distribution corresponds to a difference in touch and step voltage distribution.

In brief, in grounding system analysis at power frequency, GSA can be used in many practical situations but it tends to underestimate the results if the grid size is greater than one tenth of the wavelength of the electromagnetic field, while GSA_FD may be applied in all conditions.

      

 

 

After these conclusions a question could arise: Why not just GSA_FD?

The answer is simple but not trivial.

GSA requires an easier data entry, accept rough layouts and requires fewer computer resources.

GSA_FD requires additional information about the topology of the conductors system and in order to calculate their self and mutual impedances and a well finished layout.

Moreover GSA_FD requires more experience in the evaluation of results.

If GSA cannot be used, GSA_FD is the right solution.

 

Comparing XGSA_FD to XGSA_TD

XGSA_FD is based on the same model of GSA_FD but extended to overhead conductors. The application limits of XGSA_FD can be assumed from DC to about 100 MHz. XGSA_FD greatly expands the application field of XGS and makes it a real laboratory for engineering applications and for research.
XGSA_FD is an irreplaceable tool when conductors are partly overhead and partly underground. This situation is usual in electromagnetic fields evaluation (where sources may be underground cables or overhead wires) or interferences analysis (where often the inductor is overhead and the induced is underground).
Anyway XGSA_FD operates to a single frequency.

XGSA_TD can calculates the response in the time domain of a conductors network energized with a current or voltage transient.

As known, the methods to calculate the transient behaviour of conductors network in the time domain can be divided into two main categories: those based on the calculation of the solution directly in the time domain and those based on frequency domain calculations and then using the forward and inverse Fourier transforms.

Methods of the first category require low frequency and quasi-static approximations and in addition do not allow considering the frequency dependent characteristics of the grounding system.

Methods of the second category use an electromagnetic field approach for the calculation of the response of the grounding system in a wide range of frequencies and have a good accuracy because they are based strictly on the principles of electromagnetism. On the other hand, in these methods, a system of equations has to be solved for every particular frequency, and a large number of discrete frequency points over the frequency band are chosen to satisfy the frequency sampling theorem.

XGSA_TD is based on the second category methods and uses XGSA_FD as solver in the frequency domain. Then the application limits of XGSA_TD can be assumed as the same of XGSA_FD and in particular the maximum bandwidth of the input transient should be lower than 100 MHz.

This means that XGSA_TD can consider transient input as switching transients, standard lightning currents and also fault transients in GIS.

The simulation of lightning represents the most typical application of XGSA_TD.

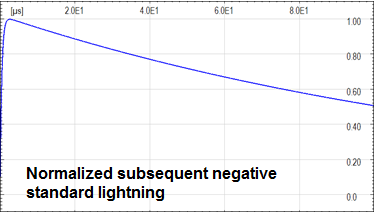
The lightning current can be simulated by using the standard short stroke wave form IEC 62305: first positive; first negative; subsequent negative.

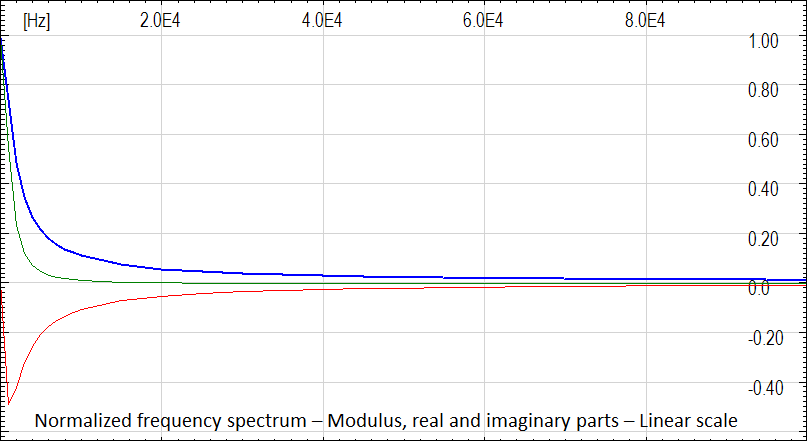
With the direct Fourier transform, the time domain input transient is decomposed in the frequency domain.

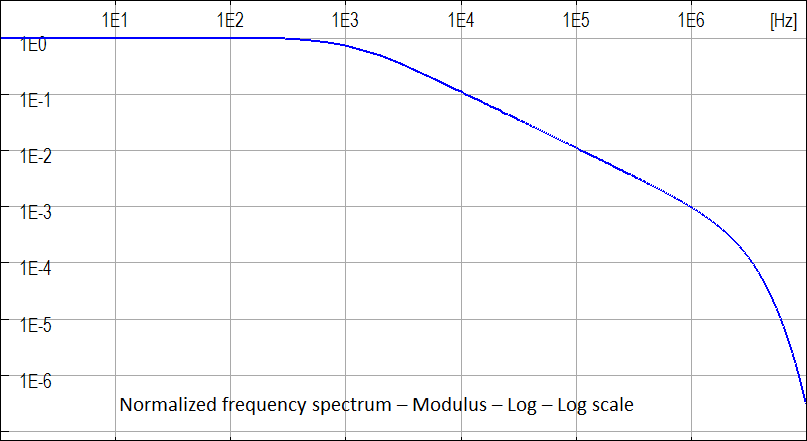
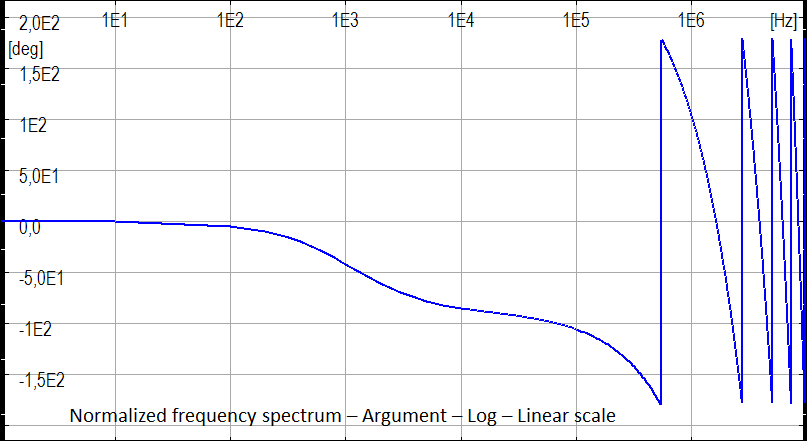
In the following figures the normalized wave shape of the subsequent negative standard lightning current and their normalized frequency spectrum. The spectrum can be neglected when normalized values are lower than about 10^-3 - 10⁴. The standard lightning bandwidth is lower than a few MHz also for the fastest lighting, the subsequent negative ones.

 

 

 

 

After the calculation in the frequency domain (taking into account a suitable number of representative frequencies in order to limits the calculation time), the response in the time domain is obtained with interpolation of results and the inverse Fourier transform.

The evaluation of lightning effects is important in many practical applications.

For instance, current generated by a stroke flows in the LPS conductors and dissipate in the soil. The electric and magnetic field generated by such high voltages and currents can cause internal discharges, fires and explosions, may cause damage of equipment and buildings and may be dangerous for people.

In conclusion, XGSA_TD uses XGSA_FD as a calculation engine and Fourier transforms in order to move from time to frequency domain and vice versa.

 

Multilayer and Multizone Soil Models

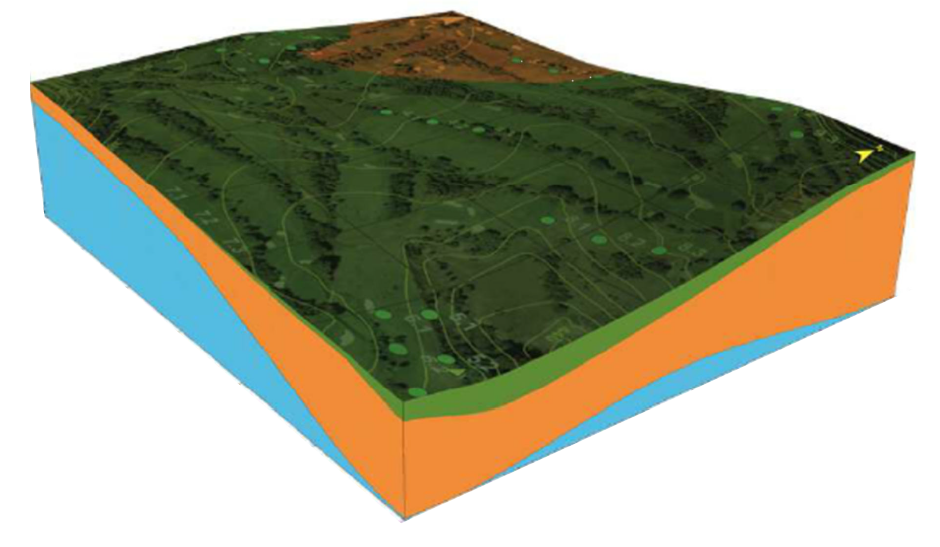
The choice of the soil model is crucial in electromagnetic simulations of systems close to the soil surface and in particular in the grounding systems analysis.

There is much literature about the criteria to set an appropriate soil model which can be used to predict the performances of a grounding system. XGS allows to use uniform, multilayer and multizone soil models.

 

 

A typical soil cross section

 

A uniform soil model should be used only when there is a moderate variation in apparent measured resistivity both in vertical and horizontal direction but, for the majority of the soils, this assumption is not valid. A uniform soil model can also be used at high frequency because in that case, the skin effect limits the penetration depth of the electromagnetic field to a few meters and so, the soil resistivity of the depth layers do not affect the results.
The soil structure in general changes both in vertical and horizontal direction and the presence of ground water further complicates things. The vertical changings are usually predominant on the horizontal ones, but about this aspect, is essential to consider also the grounding system size.
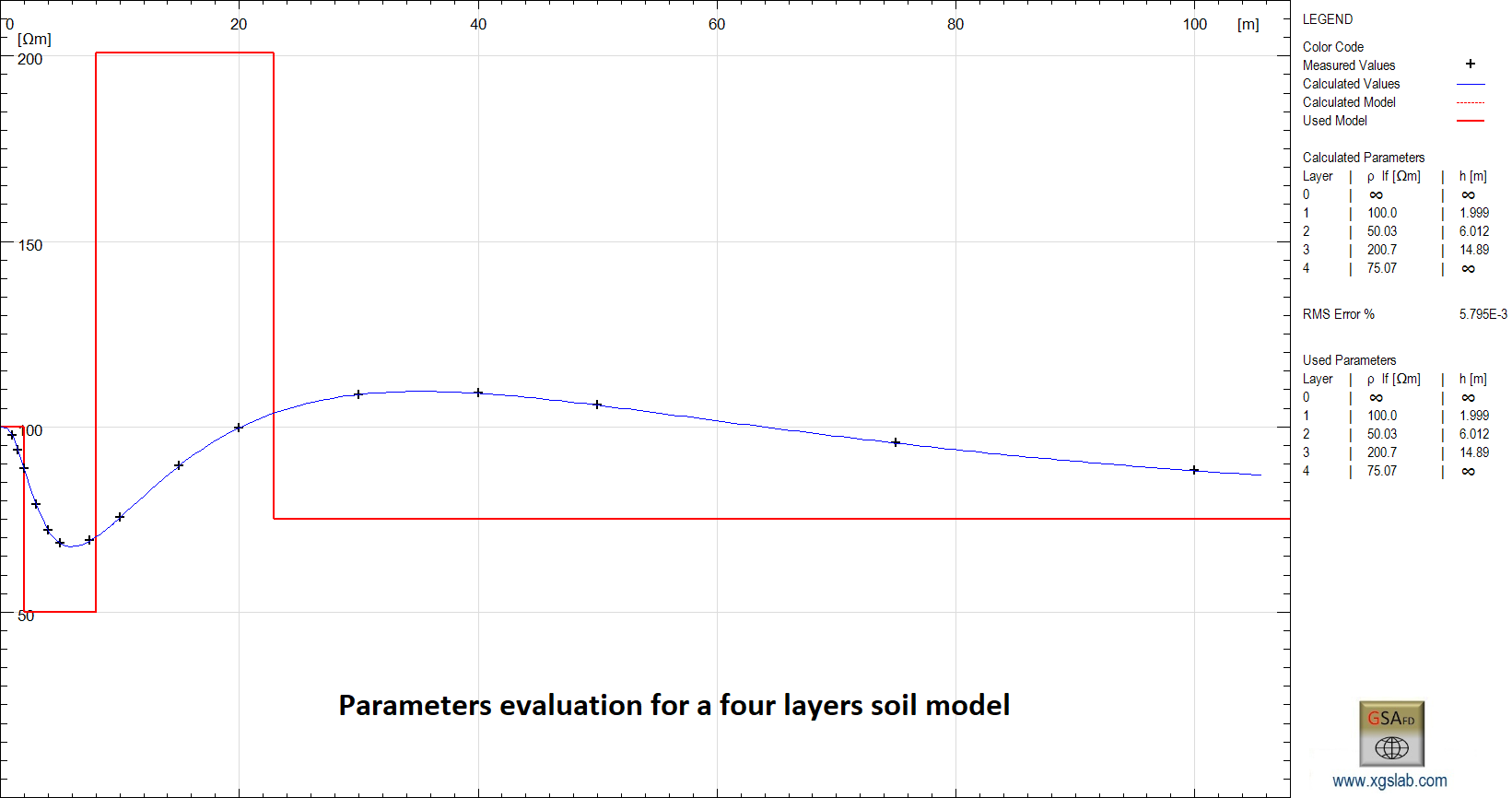
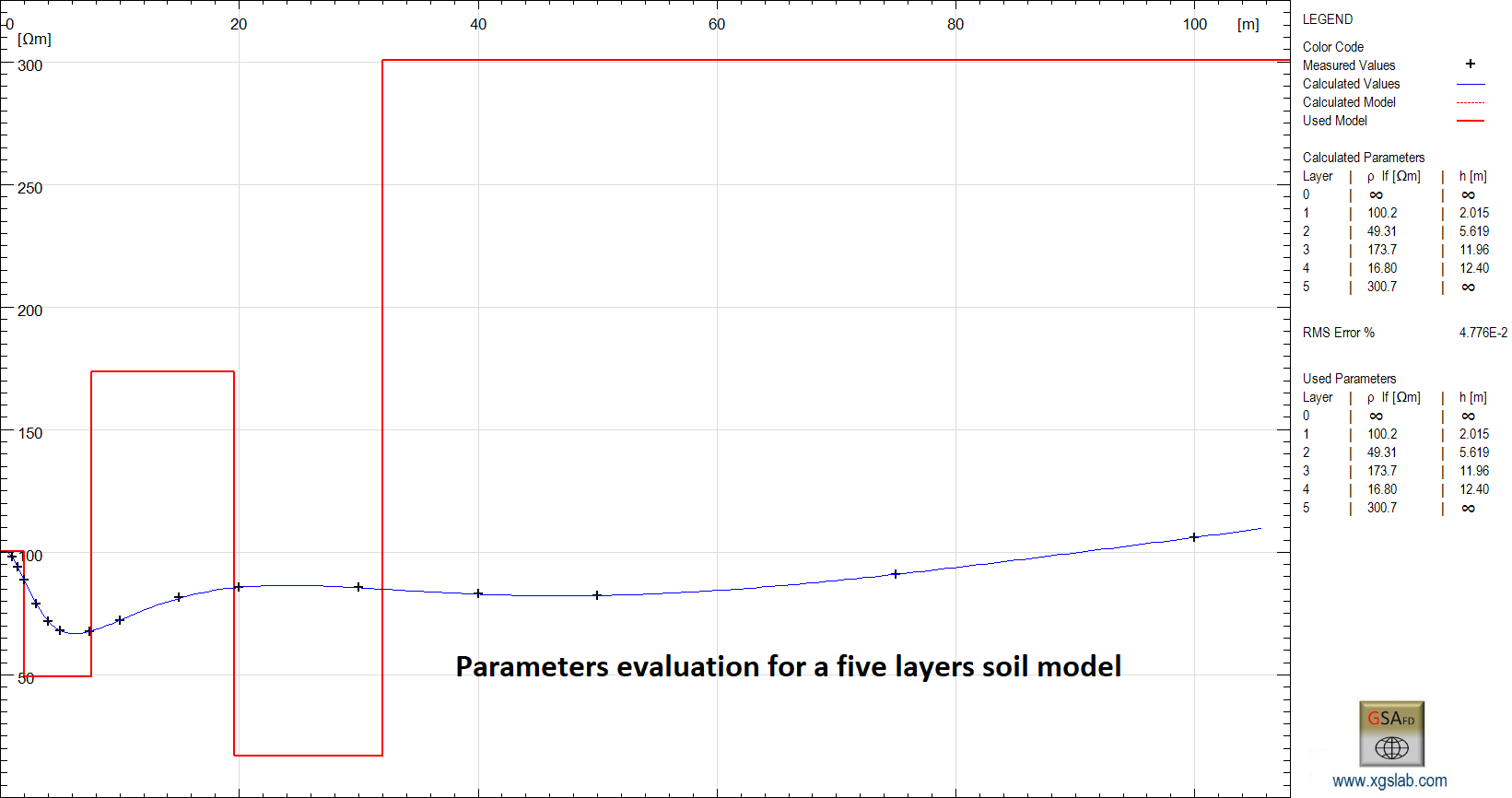
In case of small grounding systems (maximum size up to a few hundred meters), soil model is not significantly affected by horizontal changings in soil resistivity and usually a multilayer soil model is appropriate. The layer number depends on the soil resistivity variations in vertical direction and three, four or five layers can be sufficient for most cases. Sometime, in order to consider seasonal effects like frozen soil, a bigger layers number can be necessary. For this reason, XGS allows to consider up to 20 layers.

 

In case of grounding systems of intermediate size, soil model is affected by both horizontal and vertical changings in soil resistivity and usually an equivalent double or triple layer soil model is appropriate. This is the most important case in practical applications.

In case of large grounding systems (maximum size over a few kilometres), soil model is significantly affected by horizontal changings in soil resistivity and usually a multizone soil model is appropriate. The zones number depends on the systems size and soil resistivity variations in horizontal direction.

The Earth Reaction

The earth reacts to the AC electromagnetic fields.
The exact solution of this problem was found by Sommerfed and involves integrals (known as Sommerfeld integrals) that represent the solution of the Maxwell equations related to infinitesimal horizontal or vertical current elements radiating in the presence of a lossy half space. Sommerfeld integrals take into account the boundary conditions on the tangential components of the electromagnetic fields at the half space interface.
These integrals usually cannot be solved in closed form and in general are quite difficult to calculate also with a numerical approach because contain very oscillating Bessel functions.

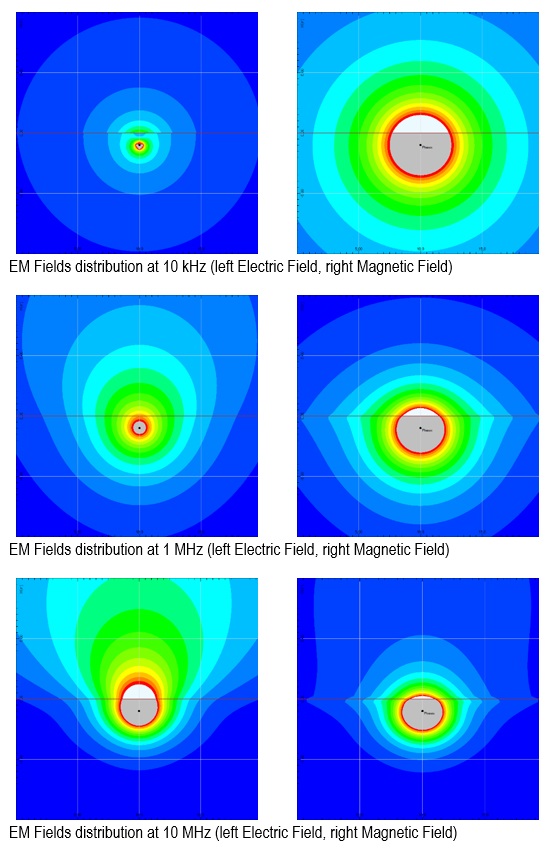
The earth reaction to the AC electromagnetic fields grows with frequency and soil conductivity and is different for horizontal and vertical buried or aerial sources.

In order to display the earth reaction in an effective way, in the following, is represented the cross section of the magnetic field close an horizontal or vertical source on or above the soil surface.

In DC condition, there is no earth reaction.

At low frequency, the earth reaction is negligible for horizontal sources but significant for vertical sources.

At high frequency, the earth reaction becomes always relevant and the earth acts as a mirror for the magnetic field. With vertical sources this happen also at relatively low frequency.

Far from the source, the earth reaction is significant also at low frequency.

The following figures show the electric and magnetic fields distributions related to a single and long overhead line at different frequencies. The calculation area is vertical and across the soil surface.

 

 

The Great Thinkers

The modules GSA, GSA_FD, XGSA_FD and XGSA_TD are based on Maxwell equations, Green functions and Sommerfeld integrals.
The module NETS is based on Kirchhoff laws.

The module SHIELD is based on Rolling Sphere and Eriksson methods.

Most people know that the electromagnetic fields are governed by a set of experimental laws known as Maxwell equations and circuits are governed by Kirchhoff laws. On the other hand, not many people know about the fundamental studies carried out by Green and Sommerfeld, about the Fourier transforms, and on the discovery made by G. Ferraris..
G. Green studied the solution of inhomogeneous differential equations and the so called Green functions are fundamental solutions of these equations satisfying homogeneous boundary conditions. 

For instance, the Green functions can be used as solutions of the Laplace equation that governs the scalar potential in a uniform or stratified propagation medium in quasi-static conditions. XGS uses the Green functions for the calculation of the scalar potential in the multilayer soil model.
A.J.W. Sommerfeld studied the earth reaction to the electromagnetic field and the rigorous solutions of the half space problem are known as Sommerfeld integrals. XGS implemented the Sommerfeld integrals for the calculation of the vector potential of horizontal or vertical electric dipoles.
Without Green and Sommerfeld studies would not have been possible to develop XGS.
Furthermore, the calculation in the time domain were been possible by using the Fourier transforms. Fourier transforms allow moving from the time domain and vice versa.

G. Ferraris was one of the pioneers of AC power systems and an inventor of the polyphase power transmission systems, induction motor and alternator, some of the greatest inventions of all ages.

 

Jean-Baptiste Joseph Fourier (Auxerre 1768 – Paris 1830)	George Green (Nottingham 1793 – Nottingham 1841)
Gustav Robert Kirkhhoff (Konisberg 1824 – Berlin 1887)	James Clerk Maxwell (Edinburgh 1831 – Cambridge 1879)
Galileo Ferraris (Livorno 1847 – Torino 1897)	Arnold Johannes Wilhelm Sommerfeld (Konigsberg 1868 – Munich 1951)
John Renshaw Carson (Pittsburgh 1886 – New Hope 1940	Sergei Alexander Schelkunoff (Samara 1987 – Hightstown 1992

 

It is also important to be grateful to the scientists and engineers that have works in this field of research as for instance J.R. Carson (1886), S.A. Schelkunoff (1897), J.R. Wait (1924) and E.D. Sunde (1927).

Of course, XGS is based on the works of other scientists and mathematician as for instance I. Newton (1643), L. Euler (1707) and J.F.C. Gauss (1777) and many others that in more recent times have improved the scientific computing.